Top 5 capital management strategies when trading options in IQ Option

Indonesia Português Tiếng Việt ไทย العربية हिन्दी 简体中文 Nederlands Français Deutsch हिन्दी Italiano 한국어 Melayu Norsk bokmål Русский Español Svenska Tamil Türkçe Zulu

Although IQtradingpro has shared many articles about how to trade in IQ Option, there’s no article specifically guiding how to manage capital in trading options. This is considered the most important factor if you want to make sustainable money in IQ Option.

Therefore, we will share top 5 capital management strategies when trading options on IQ Option in this article.

How to manage capital when trading options

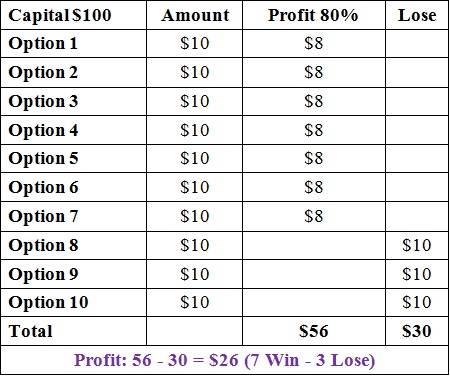
Strategy 1: Classic (Use the same amount for each option)

This is a strategy that you divide an equal amount of money on every trade.

For example, with a capital of $100 from the start, your specific goal is 10 options/day => each option will be $10.

Advantages

• No need to change the amount every time you trade.

• Your account is hard to burn (losing all money). You can only lose at a certain level.

Disadvantages

• If you want to make money with this method, you need to have an IQ Option trading strategy with a winning rate guarantee of 60% or more.

=> Classic capital management is for traders who prefer to be safe and have a high winning rate. This is the guideline for most successful traders in this market.

Strategy 2: Martingale

This is a strategy to increase capital for new options after the previous one has lost. This is how to use the next option to compensate for the lost money, plus a profit. If after a sequence of consecutive losses, a winning option will compensate for the loss of all previous losing options. As the next options will increase exponentially.

Martingale also has another name: Increase money on options when losing. If the first option loses, the second option will double or triple the money. Keep increasing until winning. Then stop and return to the starting point.

Advantages

• 1 win option can regain all previous losing options plus profits.

• Rapid profit growth.

Disadvantages

• The chance of burning your account is very high if you lose a lot of consecutive options.

• The next new options make it harder to control your emotions.

=> Martingale capital management is for adventurous investors. This is the IQ Option trading method with a winning rate of over 80%.

* Note: This strategy should stop when you have 3 losing cycles. If there is a winning option, it will end the cycle to start again. If you lose 3 consecutive options, then stop trading to avoid being trampled by the market.

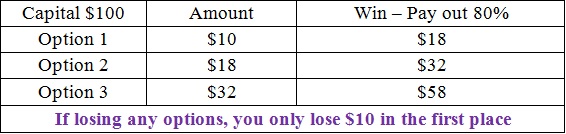
Strategy 3: Snowball (Compound interest)

In contrast to Martingale, every time you win an option, you use all the capital and interest of the first option on the next one.

For example, you deposit $10 into IQ Option. In the first trade, you WIN => Capital + Interest = 18 $. So in option 2, you will trade all $18. Just like that, the more you win the more you increase your profit.

Strength

• Accounts will grow very fast, even extremely fast

• Low starting capital. If you win 3 consecutive options you will get several times the amount of your account. But if you lose, you only lose the original capital. As in the example above, win – you get more than 5 times the starting capital. Lose – you lose $10. Suppose that you lose 5 times in a row. But with one win only, you still earn a lot of money.

Weakness

• You need to create an IQ Option trading strategy with a winning rate up to 90%. And of course, this method requires a lot of patience.

Strategy 4: Fibonacci

This is a way of managing capital in favor of defending and protecting your account. Fibonacci is an increment capital management.

For example, with Fibonacci, when you lose, increase $1. If you win, decrease $1. Details are as follows: You bet $1 and lose -> Increase to $2. If you lose again -> increase to $3. Do the same to $5 and $8 if losing.

When you bet $8 and win, reduce money to $5. Winning again => decrease to $3. Then $2 and $1.

You may be a little confused, but take it simple like this. The amount for option 3 will be equal to the total capital of options 1 and 2. Keep doing that if you lose.

But if you win, reduce the amount on the new option equal to the previous option. The more you win, the less amount you use. Therefore, your account is always in a safe state.

Strength

• The longer the cycle of losses, the shorter the cycle of winnings.

• Good emotion control because it completely eliminates the excitement when winning. You have to reduce the amount instead of increase it.

• Stable growth.

Weakness

• You have to change the amount every time you enter a trade. It may be very confusing.

Strategy 5: Using probability

This is the way to manage the capital of full-time traders. They enter a trade according to the winning probability of each option. For example, the higher the winning probability, the more amount you invest. The lower the winning probability, the less amount you use.

As a full-time trader, they have plenty of time to observe the market with different currency pairs. And they see more opportunities to open options than ordinary traders. But there aren’t always good options with a high winning rate. Therefore, they will trade with a small amount to wait for a big opportunity.

Advantages

• Flexible capital management.

Disadvantages

• Winning small-amount options is easy to cause subjective psychology. It may affect trading emotions.

• You need to experience many IQ Option trading methods to make sure which method has a high winning probability and which method has a high probability of losing.

=> This is the capital management strategy for professional traders who has many years of trading in the market.

Summary

Above are some of the ways to manage capital in options trading on IQ Option. Depending on your development, you can choose an appropriate capital management strategy.

For beginners, you only need to use $1 each option to learn and get used to the platform.
For more experienced traders, you can manage flexibly, but you have to know how to control your own emotions.

Top 5 capital management strategies when trading options in IQ Option

How to manage capital when trading options